很多人觉得概率学复杂难懂。其实概率没那么难,只不过统计学家普遍不喜欢说人话,导致阅读障碍,使得简单的问题有多种理解,从而变得复杂。很多问题归根结底是语文问题。 比如这个问题某个家庭中有 2 个小孩,已知其中一个是女孩,则另一个是男孩的概率是多少?
本文我尽量用人话解释如何用贝叶斯推断计算后验概率。
在统计学领域, 频率学派(frequentist )和贝叶斯学派(bayesian)的纷争一直不断。
频率学派认为事件发生的概率是一个确定的值, 但是这个取值我们不知道。 我们可以通过t test 或者 p 值估计这个取值的范围。
贝叶斯学派认为事件的概率是一个分布, 我们通过观测到的数据对这一分布进行更新,从而得到更为准确的估计。
首先让我们来确定本文的符号的意义。
随机变量用大写X 表示, 小写x 为随机变量X 的取值。 所以‘X=x’ 表示: 随机变量X 取值为x 这一事件。
事件A 发生的概率: \(P(A) \)
离散随机变量X的概率质量函数(pmf)为 \(p(x) \),表示离散随机变量X 取值为x 的概率为 p(x), 或者写作 \(P(X = x) = P(x) \) , 概率质量函数需要满足条件\(\sum_{x \in X}{p(x)} =1 \) .
连续随机变量X 的概率密度函数(pdf)为 \(f(x)\), 连续变量X取值在 a 和 b 之间的概率为\( P(a \leq X \leq b) = \int^a_b{f(x)} \)。 用微积分的思路推广开来, 随机变量取x 的概率为 f(x) dx 其中dx 特别小。 概率密度函数需要满足条件\int_ a^b{f(x)} = 1
pmf 和 pdf 本质上是同一个东西,只不过一个用于离散变量一个用于随机变量。
本文先来讨论先验概率为离散变量时, 应该如何更新后验概率。
用投硬币来举例子。 假设,我们有三种类型的硬币,分别是硬币ABC。 硬币ABC投出正面的概率分别为 0.5,0.6 和0.9。 我们有个抽屉, 里面放了5枚硬币,其中A类2枚,B类2枚,C类1枚。 小明从5个硬币中随机拿一枚,投一次,发现这次投出了正面。 请问, 这枚硬币最有可能是ABC类的哪一种?
这是一个典型的先验概率为离散的贝叶斯推断问题。 容我先说几句兽语:
贝叶斯公式为:
\[P(H|D)=\frac{P(D|H) \times P(H)}{P(D)}\]其中 \(H \) 是假设,\(D \)是数据,\(P(H)\)是先验概率, 先验概率顾名思义是看到数据前的猜测 。 \(P(H|D)\)是后验概率,后验概率顾名思义是拿到数据之后的猜测。 \(P(D)\) 是数据发生的概率,\(P(D|H)\)是在这个假设下数据发生的概率,也叫似然函数 。 其中\(P(D)\) 和 \(P(D|H) \)的关系是 \(P(D)= \sum_{all H}[ P(D|H)\times P(H)]\)。
用人话来分析: 小明先随机拿骰子,概率分别为0.4,0.4,0.2, 然后这三个骰子掷出正面的概率分别为0.5,0.6,0.9, 已知结果为下图画圈的H,那么小明拿到ABC 的概率分别是?
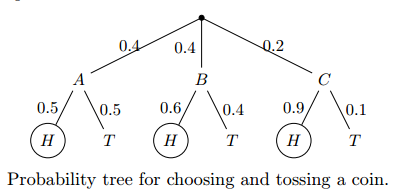
让我们回顾一下, 先验概率为
\(P(A)= 0.4 \) \(P(B) = 0.4 \) \( P(C) = 0.2 \)
那么数据为D = 正面。在ABC 三个筛子下 投出正面的概率为:
\(P(D|A)= 0.5 \)
\( P(D|B)= 0.6 \)
\(P(D|C) = 0.9 \)
我们要求已知 \(D= 正面\)的情况下,这枚硬币是ABC的概率是多少? 也就是说要比较以下三个数字的大小:
\(P(A|D)\)
\(P(B|D)\)
\(P(C|D)\)
利用贝叶斯公式, 我们还有一个变量P(D) , 不知道 , 但我们可以算, 因为“D = 正面”发生的概率是所有条件下发生“D=正面”概率的和。 用公式表示就是这样:
\[P(D) = P(D|A) \times P(A) + P(D|B)\times P(B) +P(D|C)\times P(C)\]好了,我们没有未知数了。 带入就能比较大小。
\[P(D) = P(D|A) \times P(A) + P(D|B)\times P(B) +P(D|C)\times P(C) = 0.4*0.5+0.4*0.6+0.2×0.9= 0.62\] \[P(A|D) = \frac{P(D|A) \times P(A)}{P(D)} = \frac{0.5*0.4}{0.62} = \frac{0.2}{0.62}\] \[P(B|D) = \frac{P(D|B) \times P(B)}{P(D)} = \frac{0.6*0.4}{0.62} = \frac{0.24}{0.62}\] \[P(C|D) = \frac{P(D|C) \times P(C)}{P(D)} = \frac{0.2*0.9}{0.62} = \frac{0.18}{0.62}\]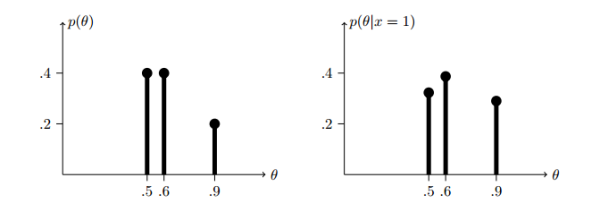
从上图我们可以看到, 已知第一次掷骰子的结果为正面, 那么小明最有可能拿到的是B类骰子。
这样我们就完成了一次贝叶斯更新。
如果小明再用这个骰子掷一次硬币,这次的结果也是正面,那么小明手里的硬币为ABC的概率分别是多少?
| 我们可以把第一次的后验概率P(A | D) 作为这次的先验概率,然后再进行一次贝叶斯更新, 计算出后检验概率。 |
带入贝叶斯公式。
\[P(A|D_1=1,D_2=1) = \frac{P(D_1=1,D_2=1|A)\times P(A)}{P(D)}= \frac{P(D_1=1|A) \times P(D_2=1|A)\times P(A)}{P(D_1=1,D_2=1)}\]同理可写出 \(P(B|D1=1,D2=1)\) 和\(P(C|D1=1,D2=1)\) 的概率。 带入数字可以得到:
\[P(A|D_1=1,D_2=1) = \frac{P(D_1=1|A) \times P(D_2=1|A)\times P(A)}{P(D_1=1,D_2=1)} = \frac{0.4*0.5*0.5}{0.4*0.5*0.5+0.4*0.6*0.6+0.2*0.9*0.9}=0.2463\] \[P(B|D_1=1,D_2=1) = \frac{P(D_1=1|B) \times P(D_2=1|B)\times P(B)}{P(D_1=1,D_2=1)} = \frac{0.4*0.6*0.6}{0.4*0.5*0.5+0.4*0.6*0.6+0.2*0.9*0.9}=0.3547\] \[P(C|D_1=1,D_2=1) = \frac{P(D_1=1|C) \times P(D_2=1|B)\times P(C)}{P(D_1=1,D_2=1)} = \frac{0.2*0.9*0.9}{0.4*0.5*0.5+0.4*0.6*0.6+0.2*0.9*0.9}=0.3990\]有的人已经发现了 。倒数第二步的分母是常数,这个常数只是为了保证所有的后验概率的和为1, 那么其实我们根本就不需要计算P(D), 只需计算分子,在扩大或缩小几倍,让他们的和为1 就行了。
这两个贝叶斯更新可以用下图表示出来
以上就是先验概率为离散数据时 更新后验概率的方法。
离散的先验概率很罕见,更常见的是连续的后延概率。 我会重新开一篇来介绍如何在连续先验概率的情况下更新后验概率。